翻译：Knuth-Morris-Pratt string matching ( KMP 字符串匹配)

点击查看英文原文

恩翻译错了也不要来打我（×）我自己都读不懂我翻了些啥……

问题：提供一个（短的）模板和一个（长的）文本，全部是字符串，判断模板是否在文本中的某处出现。上一次我们知道了如何用自动机解决这个问题。这一次我们将会通过KMP算法，一个可以被认为是十分有效的建立自动机的方法（来解决）。 我也有一些可运行的C++代码来帮你更好地理解这个算法。

现在我们来看一种简单粗暴的解决办法。
假设文本在一个数组中：char T[n]
模板在另一个数组中： char P[m]。

一种简单的方法就是尝试模板可能在文本中出现的每一个位置。

简单的字符串匹配：

有两层嵌套循环；内层花费 O(m) 次迭代（感觉不通顺啊，原文 takes one O(m) iterations），外层花费 O(n) 次迭代，所以总共的时间是他们的乘积 O(mn)。
这很慢，我们想要让他快点。
在实践中，它很好用——并不总是我们分析的 O(mn) 这样糟糕。这是因为内层循环通常会很快地发现失配的地方，不用循环 m 次就移向下一个位置。但是这种方法在一些输入下仍然会花费 O(mn) 的时间。在一种不好的情况下，像是在 T[] 中的所有字符都是 “a” ，在 P[] 中除了最后一个是 “b” 其他全是 “a”。每次进行 m 次比较结果发现没有匹配，所以总共 O(mn) 。
有个经典的例子。每行代表外层的一次迭代，行中的每个字符代表着比较的结果 （如果比较不相等即为 X ）。假设我们正在从 “banananobano” 中找模板 “nano” 。

Pos: 0  1  2  3  4  5  6  7  8  9 10 11
T:   b  a  n  a  n  a  n  o  b  a  n  o
i=0: X
i=1:    X
i=2:       n  a  n  X
i=3:          X
i=4:             n  a  n  o
i=5:                X
i=6:                   n  X
i=7:                         X
i=8:                            X
i=9:                               n  X
i=10:                                 X

一些比较就是在浪费我们的工作！例如，在迭代到 i = 2 之后，我们从比较中得知 T[3] = “a” ，所以没必要再跟 i = 3 时的 “n” 比较了。我们也知道了 T[4] = “n” ，所以也没有必要在 i = 4 时进行比较了。

跳过外层的迭代

KMP 的想法是，在这种情况下，在代码中内层循环中你做了这么多比较工作之后，你知道了文本中有什么。特别地，如果你找到了在以 i 为开始位置的一个长度为 j 的部分匹配，你就知道了在 T[i]…T[i + j – 1] 中有什么。
你可以利用这个知识用两种方法来节省工作。首先，你可以跳过一些没有可能匹配的迭代。尝试用你想要找到的匹配来重叠一些你已经找到的部分匹配：

	i=2: n  a  n
	i=3:    n  a  n  o

有两个互相冲突的放置——我们从 i = 2 时知道了 T[3] 和 T[4] 分别是 “a” 和 “n” ，所以他们不可能是 i = 3 时我们要找的 “n” 和 “a” 。我们可以一直跳到不冲突的地方。

	i=2: n  a  n
	i=4:       n  a  n  o

这里两个 “n” 相等。定义两个字符串 x 和 y 的重叠部分为 x 后缀和 y 前缀的最长单词。”nan” 和 “nano” 的重叠部分只是 “n” 。(我们不允许整个 x 或 y 是重叠部分，所以重叠部分不是 “nan” )。通常来说，我们想要跳到的 i 的值是用现在的部分匹配与最长的重叠对应的那个。

跳过迭代的字符串匹配

跳过内层迭代

在这个例子中，重叠的那个 “n” 已经在 i = 2 的时候被测试过了。没有必要再在 i = 4 的时候测试一遍了。通常来说，如果我们用最后的部分匹配找到了一个不平凡的(nontrivial)重叠，我们可以可以避免测试大量的等同于重叠部分长度的字符。
这种改进就成了（一种）KMP 算法：

KMP, 版本 1

仅剩下的细节就是计算重叠部分的函数。这是一个仅与 j 有关函数，而并不是在 T[] 中的字符，所以我们可以在我们开始这个算法之前的预处理阶段一次性计算出来。首先让我们来看看这个算法有多快。

KMP 时间复杂度分析
我们仍然有内外层循环，所以看起来时间应该还是 O(mn)。但是我们可以用一种不同的方式来看看，他事实上总是比 O(mn) 要少得多。方法是，每次我们通过内层循环，我们做一次 T[i + j] == P[j]的比较。我们可以通过数我们做了多少次比较来计算出这个算法运行的总时间。

我们把比较划分成两部分：返回 ture 的和返回 false 的。如果一次比较返回 true ，我们就会确定 T[i + j] 的值。在此后的迭代中，只要有一个包含 T[i + j] 的不平凡的重叠部分，我们会跳过那个重叠部分，不在那个位置再做比较。所以 T[] 中的每一个位置只在一次返回值为 true 的比较中被包含，总共会有 n 次这样的比较。另一方面，在外层循环中每次迭代最多会有一次返回值为 false 的比较，所以总共也会有 n 次。结果我们看到，这种 KMP 算法最多做 2n 次比较，花费 O(n) 的时间。

KMP 与 自动机
如果我们只是看看上述算法 j 发生了什么的话，它像是一种自动机。每一步中，j 被置为 j + 1 （在内层循环中，在一次匹配后）或者被置为重叠部分 o (在一次失配后)。在每一步中，j 的值只是 j 的一个函数，而不取决于其他信息像是 T[] 中的字符。所以我们可以像自动机一样画点什么，用箭头连接 j 的值和匹配和失配的标签。

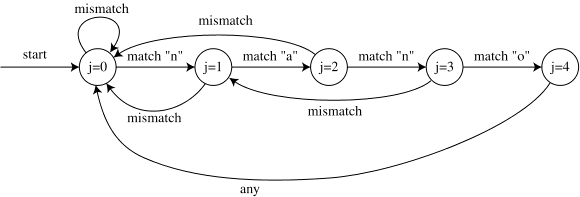
这个算法和自动机不同的地方，我们习惯说成是每一个圈，而不是每一个字符，只有两个箭头出去。但是通过在开始状态(j = 0)放置一个记号并经过箭头移动它，我们仍然可以将它比作其他自动机。每当我们在 T[] 中得到了一个匹配字符，我们移向文本的下一个字符。但是每当我们失配，我们在下一步中看相同的字符，除了在 j = 0 状态下失配这种情况。

所以在这个例子中(与上述相同)，自动机运行的状态顺序如下：

    j=0
			mismatch T[0] != "n"
    j=0
			mismatch T[1] != "n"
    j=0
			match T[2] == "n"
    j=1
			match T[3] == "a"
    j=2
			match T[4] == "n"
    j=3
			mismatch T[5] != "o"
    j=1
			match T[5] == "a"
    j=2
			match T[6] == "n"
    j=3
			match T[7] == "o"
    j=4
			found match
    j=0
			mismatch T[8] != "n"
    j=0
			mismatch T[9] != "n"
    j=0
			match T[10] == "n"
    j=1
			mismatch T[11] != "a"
    j=0
			mismatch T[11] != "n"

这本质上和上述的 KMP 伪代码的比较顺序是一样的。所以这个自动机提供了一种和 KMP 算法等同的定义。
正如一个学生在演讲(lecture)中指出的，在这个自动机中的转换并不清晰的是从 j = 4 到 j = 0 。 通常来说，从 j = m 到 j 的一些更小的值应该有一个转换，这应该在任何字符上发生(在做这个转换之前没有匹配去测试了)。如果我们想要找到模式字符串所有出现的地方，即使匹配了我们也得能继续找下去。所以例如，有个模板 “nana” ，我们应该找到它在文本 “nanana” 中所有出现的位置。所以从 j = m 的转换应该到下一个最长的能匹配的位置，简单来说就是 j = overlap(pattern, pattern)。在这种情况下 overlap(“nana”, “nana”) 是空的（所有 “nano” 的后缀都用了字母 “o” ，但是所有前缀却没有），所以跳到 j = 0 。

KMP 的替代版本
上述提到的自动机可以被翻译回伪代码，看看与之前我们看到的伪代码中不同，但却进行相同比较的部分。
KMP, 版本2

代码中每次外层循环的迭代本质上都和我在 C++ 中写的可行的实现过程相同。这个版本的优点之一是，测试字符是一个一个的，而不是在 T[] 数组中进行随机访问，所以(像是在实现中的)它可以在基于流的输入中工作而不是一股脑地先把整个文本读进内存中。

既然这个算法和另一个版本的 KMP 进行的比较相同，那么它花费的时间也相同，为 O(n) 。一种直接证明的方法就是标注(note)，首先，在每次外层循环中都有一次返回为 true 的比较(在 T[i] == P[j] 的时候)，因为当这发生的时候我们跳出了内层循环。所以共计 n 次。这些比较每一次都会使 j 增 1 。每一次我们不跳出循环的内层循环迭代执行 j = overlap[j] ，使 j 减小。因为 j 只能减小与它增加的次数相同的次数，总的时间也是 O(n)。

计算重叠部分的函数
回想一下，我们把字符串 x 和 y 的重叠部分定义为 x 的后缀与 y 的前缀的最长字母。KMP 算法剩下部分是这个计算重叠部分的函数：对于每一个 j > 0 的值我们需要知道 overlap(P[0..j – 1], P)。一旦我们计算完了这些值，我们可以把他们存在数组里，在我们需要的时候查找。为了计算重叠部分，我们需要知道字符串 x 和 y 而不只是 x 的后缀 和 y 的前缀的最长单词，它也是 overlap(x, y)的一个后缀。(显而易见地，它是一个比 overlap(x, y) 本身短的 x 的后缀。) 所以我们可以通过下面的循环来列举所有 x 的后缀和 y 的前缀。

现在我们来下另一个定义：定义 shorten(x) 是少一个字符的 x 的前缀。接下来很容易发现，shorten(overlap(x, y)) 仍然是 y 的一个前缀，但也是 shorten(x) 的一个前缀。

重叠部分计算

所以这通常给我们提供了一种递归计算重叠部分的函数。如果我们对于 x = 模式字符串的某前缀 应用这个算法，同时也应用于 y = 模式字符串本身，我们看到所有的递归调用都有相似的参数。所以如果当我们计算的时候存储下每一个值，我们可以用时查询而不是再计算一次。(这种储存而不是重计算的想法被叫做动态规划；我们曾在第一次演讲中谈到了些，下次我们会了解有关它的更多细节。)

KMP 重叠部分计算

让我们在这部分用分析 KMP 的时间复杂度来结束吧。外层循环执行 m 次。内从循环每次迭代会减小表达式 overlap[i + 1] 的值，这个表达式的值只在当我们从一层内部循环移动到下一层时增 1 。因为减少的数量最多是增加的数量，内层循环最多也是有 m 次迭代，这个算法总时间是 O(m)。

整个的 KMP 算法包括这个计算重叠部分的函数，在此之前有一个我们扫描文本的算法主部分(用重叠部分的值来加速扫描)。第一部分花费 O(m) ，第二部分花费 O(n) ，所以总时间是 O(m + n) 。

终于翻完了啊，用时 3h ，共 3307 字。